Exercise 3.4 Solution Example - Hoff, A First Course in Bayesian Statistical Methods
標準ベイズ統計学 演習問題 3.4 解答例
Answer
a
using Distributions using Plots using StatsPlots using LaTeXStrings a₀ = 2 b₀ = 8 n = 43 y = 15
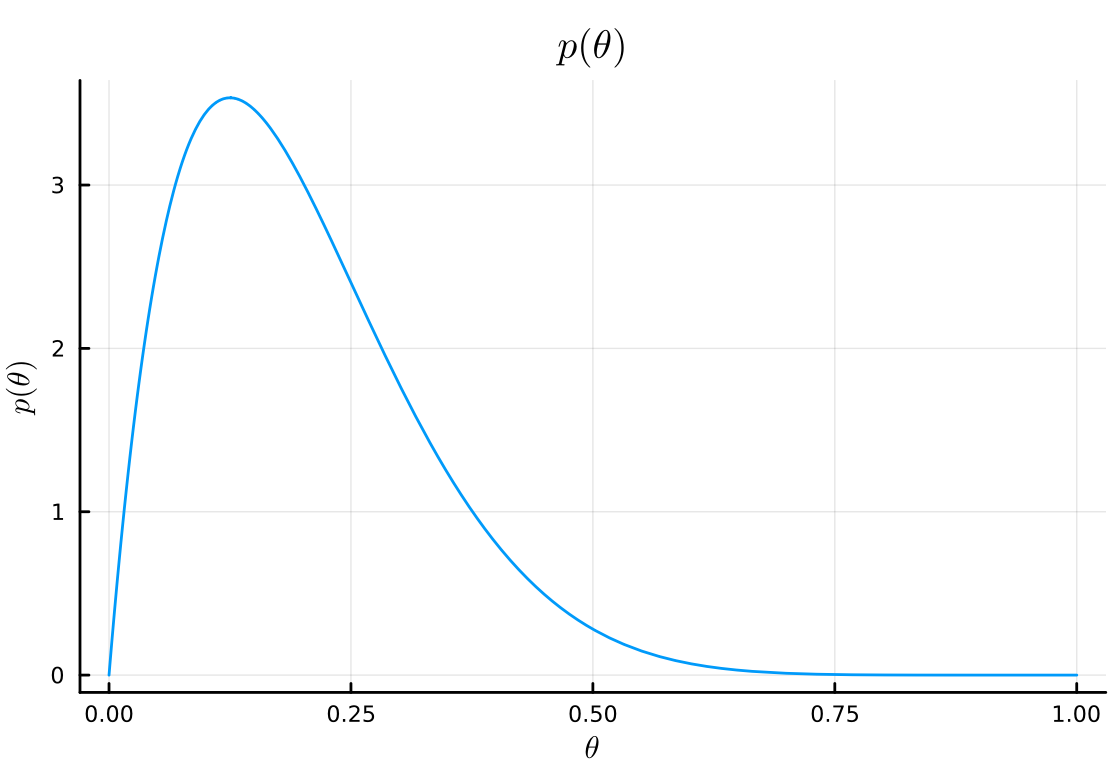
# prior plot( Beta(a₀, b₀), title=L"p(\theta)", xlabel=L"\theta", ylabel=L"p(\theta)", legend=false, )
\(y \sim \text{binomial}(43, \theta)\)より、\(p(\theta \mid y)\)を\(\theta\)の関数としてプロットすると以下のようになる。
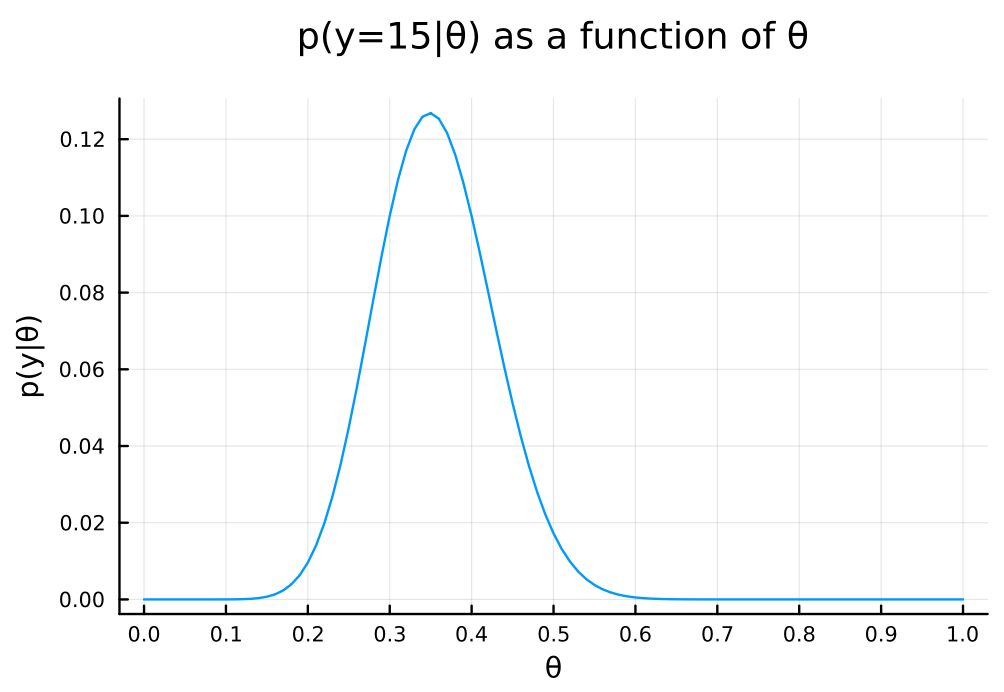
θ = 0:0.01:1.0 # 全てのθで計算 pdf_for_θs = map(θ -> pdf(Binomial(n, θ), y), θ) # plot plot( θ, pdf_for_θs, xlabel = "θ", ylabel = "p(y|θ)", title = "p(y=$y|θ) as a function of θ", legend = false, size = (600, 400) , margin = 5mm , xticks = 0:0.1:1.0 )
# posterior posterior_dist = Beta(a₀ + y, b₀ + n - y) plot( posterior_dist, title=L"p(\theta|y)", xlabel=L"\theta", ylabel=L"p(\theta|y)", legend=false, )
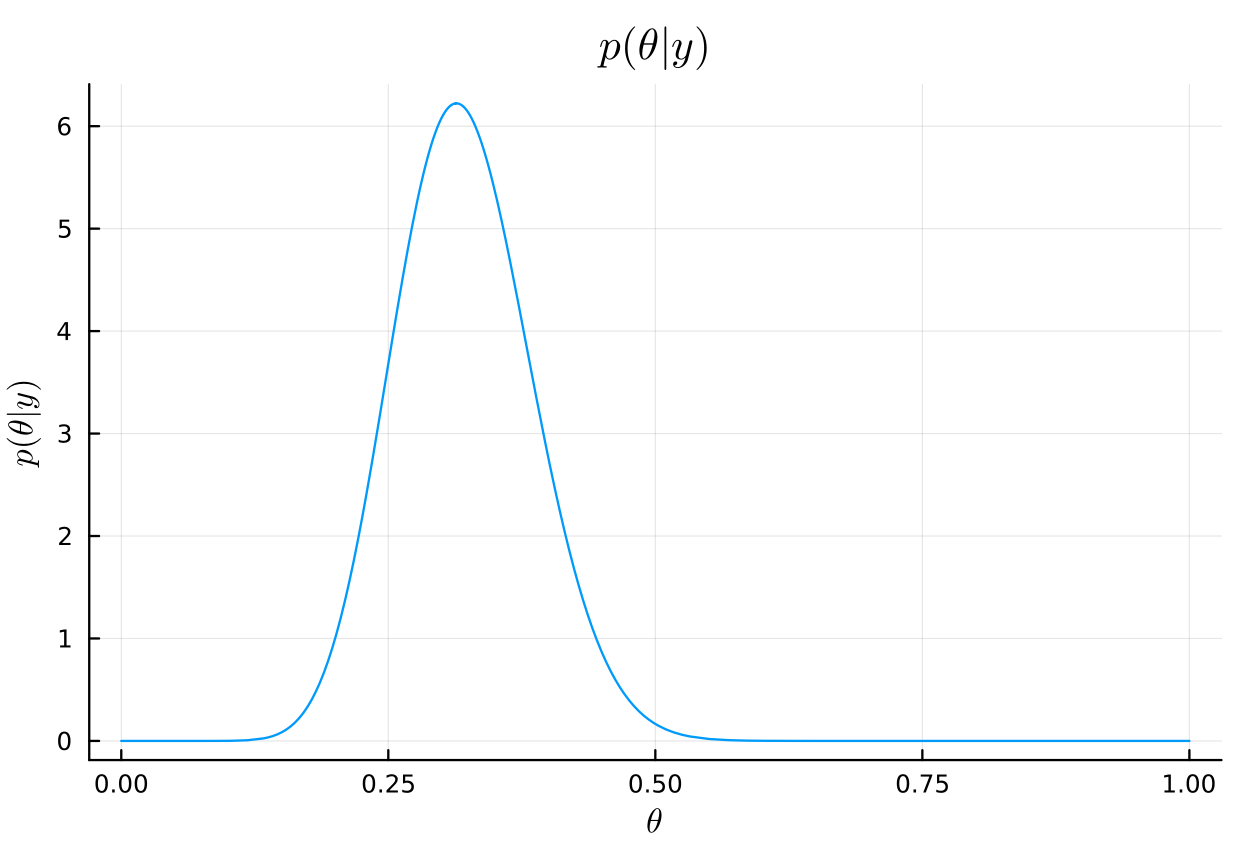
# posterior mean mean(posterior_dist) μ = (a₀ + y)/(a₀ + b₀ + n)
0.32075471698113206
# posterior mode mode(posterior_dist) (a₀ + y - 1)/(a₀ + b₀ + n - 2)
0.3137254901960784
# posterior standard deviation std(posterior_dist) var = (μ*(1 - μ))/(a₀ + b₀ + n + 1) sqrt(var)
0.0635188989834093
# posterior 95% interval quantile(posterior_dist, [0.025, 0.975])
2-element Vector{Float64}:
0.2032977878191033
0.45102398221663165
b
a₀_b = 8 b₀_b = 2
# prior plot( Beta(a₀_b, b₀_b), title=L"p(\theta)", xlabel=L"\theta", ylabel=L"p(\theta)", legend=false, )
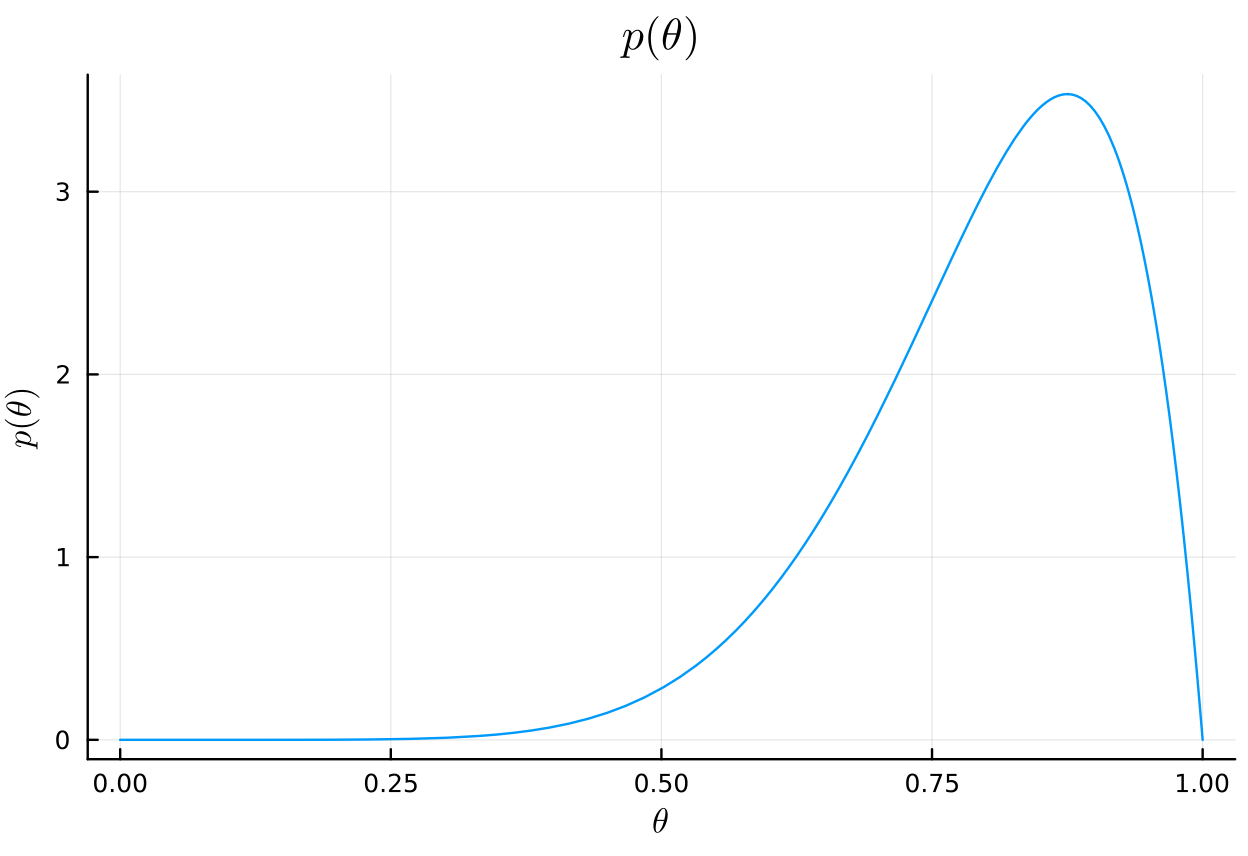
# posterior posterior_dist_b = Beta(a₀_b + y, b₀_b + n - y) plot( posterior_dist_b, title=L"p(\theta|y)", xlabel=L"\theta", ylabel=L"p(\theta|y)", legend=false, )
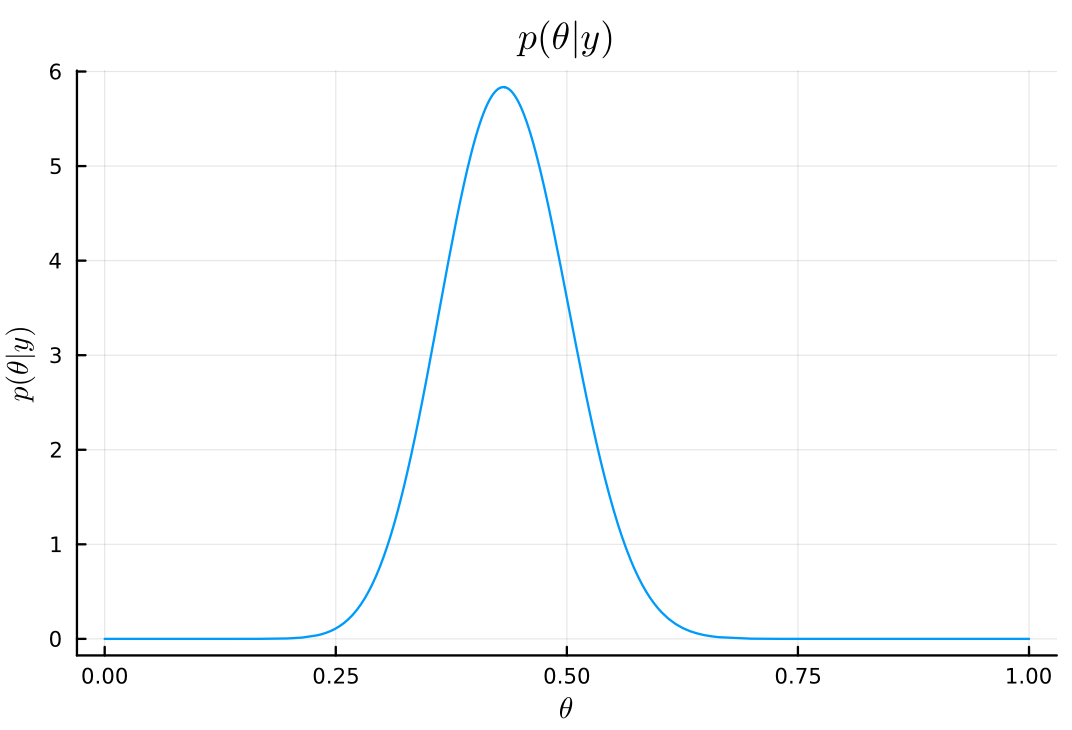
# posterior mean mean(posterior_dist_b) μ_b = (a₀_b + y)/(a₀_b + b₀_b + n)
0.4339622641509434
# posterior mode mode(posterior_dist_b) (a₀_b + y - 1)/(a₀_b + b₀_b + n - 2)
0.43137254901960786
# posterior standard deviation std(posterior_dist_b) var_b = (μ_b*(1 - μ_b))/(a₀_b + b₀_b + n + 1) sqrt(var_b)
0.06744531631926798
# posterior 95% interval quantile(posterior_dist_b, [0.025, 0.975])
2-element Vector{Float64}:
0.30469562471174694
0.5679527959964581
c
using SpecialFunctions prior_mix = θ -> 1//4 * gamma(10) / (gamma(2) * gamma(8)) * (3 * θ * (1 - θ)^7 + θ^7 * (1 - θ))
xs = 0:0.01:1.0 plot( xs, prior_mix.(xs), xlabel = "θ", ylabel = "p(θ)", title = "mixture of a beta(2,8) and a beta(8,2) prior distribution", titlefontsize = 12, legend = false, size = (600, 400) , margin = 5mm , xticks = 0:0.1:1.0 )
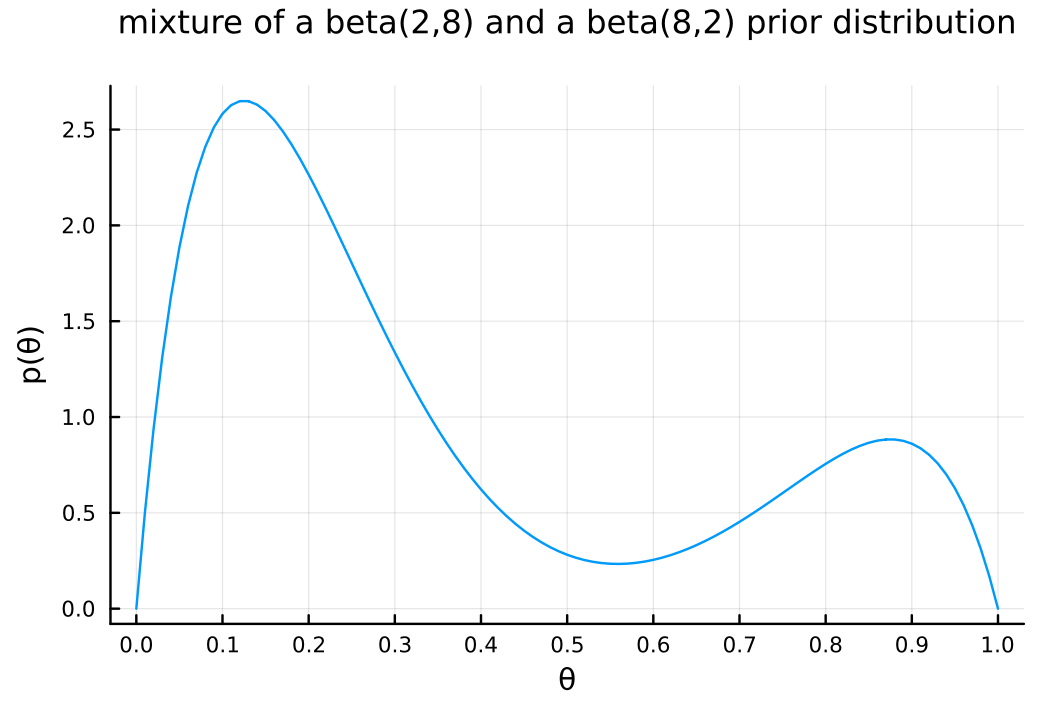
aやbの事前分布と異なり、上の分布は 2 つの山を持った形状になっている。この事前分布は、再犯率は高いか低いかのどちらかに偏っているという信念を表している。
d
For the prior in c):
i
Write out mathematically \(p(\theta) \times p(y \mid \theta)\) and simplify as much as possible.
Answer:
\begin{align*} p(\theta) \times p(y \mid \theta) &= \frac{1}{4} \frac{\Gamma(10)}{\Gamma(2)\Gamma(8)} [3 \theta (1-\theta)^7 + \theta^7 (1-\theta)] \times \begin{pmatrix} 43 \\ 15 \end{pmatrix} \theta^{15} (1-\theta)^{28} \\ &= \frac{1}{4} \frac{\Gamma(10)}{\Gamma(2)\Gamma(8)} \begin{pmatrix} 43 \\ 15 \end{pmatrix} \left[3 \theta^{1+15} (1-\theta)^{7+28} + \theta^{7+15} (1-\theta)^{1+28}\right] \\ &= \frac{1}{4} \frac{\Gamma(10) \Gamma(44)}{\Gamma(2)\Gamma(8) \Gamma(16) \Gamma(29)} \left[3 \theta^{16} (1-\theta)^{35} + \theta^{22} (1-\theta)^{29}\right] \\ \end{align*}ii
The posterior distribution is a mixture of two distributions you know. Identify these distributions.
Answer:
Beta(17, 36) and Beta(23, 30)
iii
On a computer, calculate and plot \(p(\theta) \times p(y \mid \theta)\) for a variety of \(\theta\) values. Also find (approximately) the posterior mode, and discuss its relation to the modes in a) and b).
Answer:
cond_prob = θ -> pdf(Binomial(n, θ), y) prior_times_cond_prob = θ -> prior_mix(θ) * cond_prob(θ) xs = 0:0.001:1.0 plot( xs, prior_times_cond_prob.(xs), xlabel = "θ", ylabel = "p(θ) × p(θ|y)", title = "p(θ) × p(θ|y)", legend = false, )
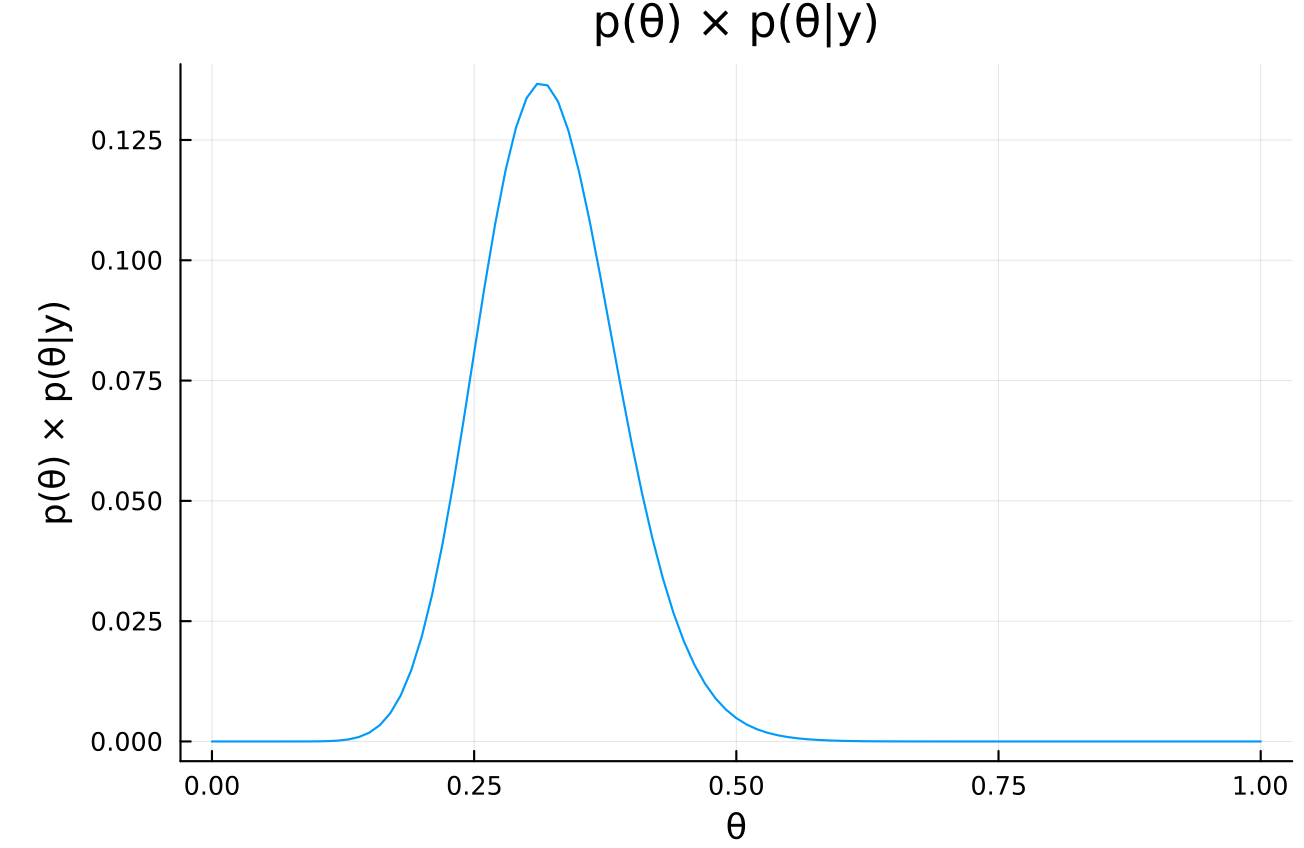
# prior_times_cond_probが最大になるθ xs[argmax(prior_times_cond_prob.(xs))]
a) の mode が 0.313,b)の mode が 0.431 であったので、この事後 mode はその中間（かなり a より)に位置している。
e
Find a general formula for the weights of the mixture distribution in d)ii, and provide an interpretation for their values.
Answer:
\(n ,y\)一般に対し、事後分布は
\begin{align*} p(\theta \mid y) &= \frac{p(y \mid \theta) p(\theta)}{p(y)} \\ & \propto p(y \mid \theta) p(\theta) \\ &= \begin{pmatrix} n \\ y \end{pmatrix} \theta^y (1-\theta)^{n-y} \times \frac{1}{4} \frac{\Gamma(10)}{\Gamma(2)\Gamma(8)} \left[3 \theta (1-\theta)^7 + \theta^7 (1-\theta)\right] \\ & \propto 3 \theta^{y+1} (1-\theta)^{n-y+7} + \theta^{y+7} (1-\theta)^{n-y+1} \\ & \propto \frac{3}{4} \theta^{y+2-1} (1-\theta)^{n-y+8-1} + \frac{1}{4} \theta^{y+8-1} (1-\theta)^{n-y+2-1} \\ &= \frac{3}{4} \text{dbeta}(y+2, n-y+8) + \frac{1}{4} \text{dbeta}(y+8, n-y+2) \end{align*}となる。よって事後分布は、Beta(y+2, n-y+8) と Beta(y+8, n-y+2)を 3 対 1 の重みをつけて混合させたものが事後分布となる。
